UNIDAD Nº 1: Los números reales

- Números enteros en la recta numérica.

• Conjunto de números enteros (): Está formado por los números naturales, sus opuestos y el cero.

Todos los números pueden ordenarse en una recta numérica. De esta manera, podemos determinar si un número es mayor o menor que otro, dependiendo del lugar que ocupa en la recta numérica. 

Para representar números como puntos de una recta puedes proceder de esta manera:

-Trazas una recta horizontal y sobre ésta marcas un punto. A ese punto lo llamas 0.

- Eliges una medida cualquiera (no demasiado grande para que puedas ubicar varios números) y la utilizas como distancia para marcar el 1 a la derecha del 0, el 2 a la derecha del 1, etcétera. Recuerda, la distancia entre los números debe tener la misma medida:

Decimos que un número es menor, cuando está ubicado a la izquierda de otro en la recta numérica, o sea, está más cerca del 0 y, decimos que es mayor, cuando se ubica a la derecha de otro y está más alejado del cero. Puedes ver que el número 3 está más alejado del 0, es el número más grande que ubicamos en la recta.

♥ Ejercicios: 

1. En la siguiente recta están ubicados el 0 y el 8. ¿Dónde se ubica el número 5? ¿Dónde se ubican los números -1 y -2?
2. En la siguiente recta están ubicados los números 0; 1 y a. ¿Dónde se ubicaran los números a-1; -a y   -a+1?

♥ Resoluciones: 

1.  

2.
 

Noción de opuestos o inverso aditivo.

El inverso aditivo de un número es el opuesto de ese número, esto es, el inverso aditivo de un número x es - x. La suma de un número y su inverso aditivo siempre es cero, eso es, x + (-x) = 0. 


- Números racionales en la recta numérica.

• Conjunto de números racionales (): Está formado por todos los números que pueden ser expresados como fracción (es decir como cociente de dos números enteros) o mediante expresiones decimales (con parte decimal finita o parte decimal periódica).

-Para ubicar fracciones, divides el entero (o los enteros) en tantas partes como indica el denominador y tomas las que indica el numerador.
Por ejemplo:
                                 

La fracción 3/5 se ubica en la recta, en el punto amarillo. El segmento de recta que representa al número 1 lo dividimos en cinco partes que están indicadas de color rojo. De esas cinco partes, tomamos las tres que están señaladas con color azul.
Si prestas atención verás que el número 3/5 está más cerca del 0, por lo tanto es más pequeño que el número 1.

Diferentes formas de representación de números racionales: fracciones y expresiones decimales.

Para representar números decimales en la recta numérica debemos primero transformalos a fracción y luego podremos graficarlos como ya hemos aprendido anteriormente.
Veamos los siguientes números decimales:
0,3 y 2,45
Al leerlos tenemos:
0,3 = tres décimos, ya que, después de la coma tenemos 1 cifra. Si lo representamos como fracción tenemos 

Para representar el decimal 0,7 observamos que es número comprendido entre el 0 y 1. Dividimos el segmento en unidad entre los números 0 y 1 en 10 partes iguales y tomamos 7 de esas partes contando a la derecha ( ya que 0,7 es positivo) desde el cero.

♥ Ejercicios:

1. Ubica -1 en la recta que sigue:

2. Ubica 3/4 en la recta que sigue:

♥ Resoluciones: 

1. 

2. 

- Números irracionales en la recta numérica.

• Conjunto de números irracionales (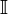): Está formado por aquellos números cuyo desarrollo decimal es infinito (), es decir que no se pueden expresar como fracción.

 ♥ Ejercicios:

1. Ubicar el número √2 en una recta numérica. Demostrar que √2 no es un número racional.
2. ¿Existe algún número irracional cercano a √2? ¿Y alguno que se encuentre próximo al número π? Justificar cada respuesta.
3. Determinar, en cada caso, si es posible escribir a los siguientes números como fracción. Justificar. Luego ubicar en la recta numérica dichos números.    a.  √5    b.  √7    c.   √9/4

- Conjunto de los números reales.

• Números reales (): Conjunto formado por los números naturales, los enteros, los racionales y los irracionales. 

Distancia entre números e intervalos de números

En una recta numérica se pueden ubicar todos los números reales. A cada número real le corresponde un punto de la recta, y a cada punto de la recta le corresponde un número real. Es decir, los números reales completan la recta numérica.

A la recta numérica se la conoce como eje real.

 =   

   =    

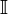
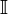(entre Q y II no hay nada)

1.  Todos los números que están a la derecha de m (son números b mayores que m).

Se escribe:  b  (m; +∞) Sí b > m

2.  Los números b que se ubican a la izquierda de -m tienen también una distancia al cero mayor que m

Se escribe: b  (-∞;+∞) Sí b <  -m

Conclusión: El conjunto de todos los números reales "b" que verifican que la distancia al cero es mayor que "m" esta formado por los números menores que "-m" o que sean mayores que "m"

Simbólicamente:

(-∞;-m)  (m;+∞)

1 ♥ Se denomina intervalo abierto a la escritura (a ; b) y significa que se consideran todos los números reales X que se encuentran entre a y b

Simbólicamente:  X ∈ (a ; b) Sí a < X < b
Ejemplo: Números reales mayores que 3 y menores que 7

3 < X < 7       

(3 ; 7)

2 ♥ Se denomina intervalo cerrado a la escritura [a ; b] y significa que se consideran todos los números reales X que se encuentran entre a y b incluyendo al a y al b.

Simbólicamente: X ∈ [a ; b] Sí a ≤ X ≤ b
Ejemplo: Idem. al 1 pero incluyendo a los números 3 y 7.

3 ≤ X ≤ 7

[3 ; 7]

3 ♥ Para designar a todos los números reales mayores que m se escribe (m;+∞). Analógicamente, el intervalo que contiene a todos. Los números menores que m es (-∞;m)

Ejemplo: Números reales mayores o iguales que -1

X ≥ -1 

[-1 ; +∞]

NOTA: Si un intervalo se incluye sólo uno de los extremos, se dice que es intervalo es

SEMIABIERTO o SEMICERRADO

Ejemplo: Números reales mayores o iguales a -5 y menores a 2

-5 ≤ X < 2

[-5 ; 2)

Módulo 

Se llama módulo o valor absoluto de un número real a la distancia que hay entre el número y el 0.

Simbólicamente: Sea con X un número real su módulo se escribe I X I (barras de módulo).

Ejemplo: 

  

I -4 I = 4

I -1 I = 1

I 0 I = 0

I 1 I = 1

I 4 I = 4

♥ 1ra propiedad: Sí X ∈ a  se verifica en:
I X I es mayor o igual a 0 
I X I ≥ 0 

I C I = 9 
C = 9 ó C = -9 

♥ 2da propiedad: Sea a un número real positivo...

I C I = a              • Lecturas:  C = a  C = -a 

I C I < 9  (números reales cuyo módulo de menor a 9 distancia a 0).

De los números negativos verificar los mayores a -9.       C > -9

De los números positivos verificar los menores que 9.    C < 9

I C I < 9 entonces  -9 < ⊂ < 9     C ∈ (-9 ; 9)

♥ 3ra propiedad: 

I C I < 9 entonces  -9 < ⊂ < 9     C ∈ (-9 ; 9)

I C I > 9 (números reales cuyo módulo distancia al 0, sea mayor a 9).

I C I  > 9 entonces,  C > 9 ó C < -9  o sea, C ∈ (-∞ ; -9) ∪ (9 ; +∞)

♥ 4ta propiedad: 

I C I > a  entonces, C > a    C < -a  o sea, C ∈ (-∞ ; -a) ∪ (a ; +∞)

Programa de Matemática

UNIDAD Nº 1: Los números reales

• Los números enteros en la recta numérica. Las letras para representar números genéticos. El conjunto de números enteros. Relación de orden en Z. Noción de opuesto o inverso aditivo.
• Los números racionales en la recta numérica. Diferentes formas de representación de números racionales: fracciones y expresiones decimales. El conjunto de los números racionales. Relación de orden y desidad en Q.
• Los números irracionales en la recta numérica. Demostración de la no racionalidad de √2. Definición de número irracional. Encuadramiento de números irracionales.
• El conjunto de los números reales. Definición a partir de las relaciones de inclusión de completitud.
• Distancia entre números reales e intervalos de números. Módulo de un número real. Propiedades del módulo.

UNIDAD Nº 2: Ecuaciones e inecuaciones

• Ecuaciones lineales con una variable. Conjunto solución y ecuaciones equivalentes. Propiedades. Ecuaciones lineales con infinitas soluciones y sin solución.
• Resolución de ecuaciones en N, Z, Q y R.
• Inecuaciones lineales con una variable. Conjunto solución. Propiedades.
• Ecuaciones e inecuaciones con módulo.

UNIDAD Nº 3: Estudio de funciones

• Interpretación de gráficos y tablas que expresan relaciones entre magnitudes variables.
• Definición de función a partir de la terna dominio, codominio y ley de correspondencia. Imagen, preimagen y conjunto imagen.
• Estudio de funciones a partir de su gráfica. Conjunto de ceros, de positividad y de negatividad. Ordenada al origen. Intervalos de crecimiento y decrecimiento. Máximos y mínimos.
• Producción e interpretación de fórmulas para representar funciones. Notación simbólica f : A → B / y = f (x). Estudio de funciones a partir de su fórmula. Noción de función inversa.
• Sucesiones: Término general de una sucesión.

UNIDAD Nº 4: Funciones y ecuaciones cuadráticas

• El modelo cuadrático. La función cuadrática f : R → R / f (x) = x². Representación gráfica: la parábola. Características del gráfico: eje de simetría, vértice.
• Desplazamientos de la gráfica. Expresión canónica de la función cuadrática.
• Intervalos de crecimiento y decrecimiento. Conjuntos de positividad y negatividad. Máximos, mínimos y ceros. Concavidad.
• Resolución de ecuaciones cuadráticas. Análisis del discriminante.
• Expresión polinómica y factorizada de la función cuadrática.
• Estudio completo de funciones cuadráticas. Problemas de máximos y mínimos.
• La parábola como lugar geométrico.

UNIDAD Nº 5: Polinomios

• Definición. Término principal y término independiente. Coeficiente principal. Grado. Polinomio mónico y polinomio nulo. 
• Operaciones con polinomios: suma, resta, producto y cociente.
• Raíces reales de un polinomio. Multiplicidad de las raíces. Teorema del resto. Regla de Ruffini. 
• Polinomios expresados como producto. Factor común, trinomio cuadrado perfecto, diferencia de cuadrados. Teorema de Gauss. Factorización.

UNIDAD Nº 6: Combinatoria y probabilidad

• Problemas de conteo. Diagrama de árbol. Factorial de un número. Permutaciones y variaciones con y sin repetición. Combinaciones. Número combinatorio. Binomio de Newton.
• Probabilidad: Experimento aleatorio, espacio muestral y sucesos. Definición de Laplace. Sucesos seguro, imposible y excluyentes. Cáculo de probabilidad de un suceso. Propiedades.

Prof. Darío Wejchenberg

Funciones Cuadráticas (10)

Problema 10
Dada la función f(x) = (x+3)² - 9
A) Decidir, en cada caso, si es cierta la afirmación:
        l) Hay dos valores de x tales que f(x) = 160
        ll) Hay dos valores de x tal que f(x) = 5
        lll) Hay dos valores de x tal que f(x) = -20
B) Para cada una de las siguientes frases, completarlas con un número para que resulten verdaderas:
        l) Hay un único valor de x tal que f(x) = .........
        ll) No hay valor de x tal que f(x) = ........
        lll) Hay tres valores de x tales que f(x) = ........
C) Hacer un gráfico aproximado de la función f.

Resolución:
A. l) Sí, 10 y -16

    13² = 169
(-13)² = 169


Verdadero





ll)

Verdadero






lll)

Absurdo, porque los cuadrados siempre son positivos (o cero) 

B. l) -9 (en x = -3)
    ll) -17; -16; -15; -14;..
    lll) No se puede completar con nada.

C. Conjunto Imagen: Conjunto de todos los valores que toma la cuenta [-9 ; +∞)

Ordenada al origen
(intersección con eje Y)
Es la imagen de x = 0

Funciones Cuadráticas (9)

Problema 9
Dadas las siguientes funciones, hallar el máximo o el mínimo valor que puede alcanzar cada una de las funciones y en qué valor de x lo alcanza.
a) f(x)=(x+5)²-4
b) g(x)=5-(4x+3)²
c) h(x)=(7x-5)²+18

Resolución:

Término cuadrático
Término constante

a. f(x)=(x+5)²-4

Mínimo: -4 en x= -5  
El término cuadrático está sumando; entonces hay un mínimo.

b. g(x)=-2(x-5)²+1

Máximo: 1 en x= 5
El término cuadrático está restando; entonces hay un máximo.

c. h(x)=5-(4x+3)²

Máximo: 5 en x= -3/4
El término cuadrático está restando; entonces hay un máximo.

d. i(x)=(7x-5)²+18

Mínimo: 18 en x= 5/7
El término cuadrático está sumando; entonces hay un mínimo.

Los "cuadrados" son siempre positivos (o cero). 
El máximo/mínimo ocurre cuando se anula ("da cero") el término cuadrático.

-------------------------------------------------------------------------------------------------------------

Las expresiones de las formas

F(x) = a (x + b)² + c

a tiene que ser distinto a cero; si es cero, al multiplicarse con el término cuadrático desaparece y no es más cuadrado.

Funciones Cuadráticas (8)

Problema 8
Dada la siguiente función f(x)=(x-2)²+4

a) Busque, si existen, otros valores de dominio que tengan la misma imagen que x=5. ¿Cuántos hay?
b) Busque, si existen, otros valores de dominio que tengan la misma imagen que x=-3. ¿Cuántos hay?
c) Busque, si existen, otros valores de dominio que tengan la misma imagen que x=2. ¿Cuántos hay?
d) Propongan, si existe, valores de dominio cuya imagen sea 13. ¿Cuántos hay?
e) Propongan, si existen, valores de dominio cuya imagen sea 3. ¿Cuántos hay?
f) Propongan, si existen, valores de dominio cuya imagen sea 4. ¿Cuántos hay?
g) Analicen cuales de los siguientes gráficos podría corresponder a la función analizada.

Resolución

a) Uno más (-2). Porque con este número cuando lo que esta en paréntesis es elevado al cuadrado de 9+4=13
b) Uno más (7).(7-2) ²+4=24  /   (-3-2) ²+4=29
c) No hay ninguno, porque no hay otro valor que al restarle 2 me de 0, entonces la ecuación no dará lo mismo.
d) Valores del dominio cuya imagen sea 13: 5 y -1
e) Valores del dominio cuya imagen sea 3. 

• Porque (x-2)² es siempre positivo o cero, y (x-2)² se le está sumando a 4.
• Porque el mínimo valor que toma la cuenta es 4
• No hay valores de x cuya imagen de 3; para que sea 3 (x-2)² tiene que ser -1. Pero no puede ser negativo por que es un cuadrado.  

(x-2)²=-1  

ABSURDO MATEMÁTICO 

f) Valores de dominio cuya imagen sea 4

4=(x-2)²+4

Entonces, (x-2)²=0

x-2=0

x=2

Está e mínimo de la función.

g)  • Gráfico 4: No corresponde porque la función no tiene valores negativos de Y.

     • Gráfico 5 y 2: No corresponde porque el mínimo valor se produce en 2 (no en un número negativo)

     • Gráfico 1: No corresponde porque la función no tiene máximo, tiene un mínimo.

     • Gráfico 3 y 6: No corresponde porque no poseen simetría 

PARA RECORDAR:

• Hay valores de la variable Y que son imagen de dos valores de X compañeros (por ejemplo: el 13 es la imagen del 5 y del -1)
• Hay un único valor de Y que es imagen de un solo valor de X (por ejemplo: el 4 tiene como imagen solo el 2)
• Hay valores de Y que no son imagen de ningún valor de X (por ejemplo: 3; 2; 1; ...)

Para miércoles 10

Tarea para miércoles: Terminar problema 8

No se olviden de entregar tareas pendientes y resúmenes de clase!

Funciones cuadráticas (1)

Problema 1

Se arma con fósforos un cuadrado cuadriculado de la siguiente forma:

1. ¿Cuantos fósforos se necesitan para armar esta figura?
2. ¿Cuantos fósforos se necesitan para armar un cuadrado que tenga 56 fósforos de lado?
3. Encontrá una formula que permita calcular la cantidad de fósforos que se necesitan para armar un cuadrado de N fósforos de lados. 

Resolución

1. Se necesitan 24 fósforos
2. Se van a necesitar 6384 fósforos. Ceunta realizada: 56+1=57       57x56=3192       3192x2=6384
3. Una fórmula que se puede utilizar es la siguiente: L(L+1)x2. En este caso L debe ser reemplazado por la cantidad de fósforos de lado que tiene el cuadrado.

OBJETIVO

Este blog posee el fin de poder plasmar las cosas que se trabajan en las clases. En el se podrán encontrar:

• Resúmenes de clase
• Tarea
• Actividades de repaso
• Fecha de evaluaciones o trabajos.
• Sección preguntas (consiste en hacer preguntas de la materia al grupo, para que luego se las hagan al profesor y así poder contestarlas en una entrada nueva).
• Videos explicativos